Introduction
Back in 2015 I published an article [1] about the QR decomposition of a centrosymmetric real matrix. In 2016 I started thinking about the meaning of this decomposition and centrosymmetric matrices in general. I discovered that centrosymmetric matrices have a natural interpretation as split-complex matrices and even more, that the centrosymmetric QR decomposition of a matrix actually corresponds to a QR decompositon of a split-complex matrix for which the original matrix is it representation. In a certain sense, the centrosymmetric QR decomposition introduced in [1] of a real square matrix of order 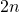 is equivalent to a QR decomposition of a corresponding split-complex square matrix of order
is equivalent to a QR decomposition of a corresponding split-complex square matrix of order 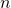 . All these notions will be made precise in the following sections. This blog post is based on my own preprint.
. All these notions will be made precise in the following sections. This blog post is based on my own preprint.
Matrix representations
If 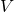 is a finite-dimensional vector space then we denote by
is a finite-dimensional vector space then we denote by 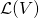 the set of all linear transformations
the set of all linear transformations 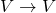 . Recall that if
. Recall that if 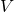 is an
is an 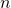 -dimensional vector space and
-dimensional vector space and 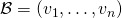 an ordered basis for
an ordered basis for 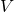 , then every linear transformation
, then every linear transformation 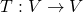 has an
has an 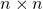 matrix representation with respect to
matrix representation with respect to 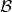 denoted
denoted ![Rendered by QuickLaTeX.com [T]_\mathcal{B}](https://konrad.burnik.org/wordpress/wp-content/ql-cache/quicklatex.com-9681ac63ba28fe01a34082b913969eed_l3.png) . Further, for any two linear transformations
. Further, for any two linear transformations 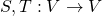 we have
we have ![Rendered by QuickLaTeX.com [S \circ T]_\mathcal{B} = [S]_\mathcal{B} [T]_\mathcal{B}](https://konrad.burnik.org/wordpress/wp-content/ql-cache/quicklatex.com-f8a34a6154bbdcbec92f422ac7a4f5bb_l3.png) . The standard ordered basis for
. The standard ordered basis for 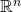 i.e. the basis
i.e. the basis 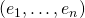 is defined as
is defined as 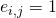 if
if 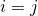 and
and 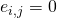 otherwise.
otherwise.
An algebra 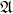 is an ordered pair
is an ordered pair 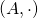 such that
such that 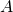 is a vector space over a field
is a vector space over a field 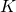 and
and 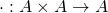 is a bilinear mapping called multiplication.
is a bilinear mapping called multiplication.
Let 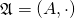 be an algebra. A representation of
be an algebra. A representation of 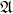 over a vector space
over a vector space 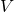 is a map
is a map 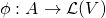 such that
such that
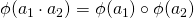 for all
for all 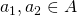 .
.
Let 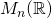 denote the set of
denote the set of 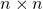 real matrices. If
real matrices. If 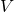 is an
is an 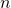 -dimensional vector space and
-dimensional vector space and 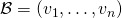 an ordered basis for
an ordered basis for 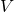 then every linear transformation
then every linear transformation 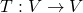 has a matrix representation
has a matrix representation ![Rendered by QuickLaTeX.com [T]_\mathcal{B} \in M_n(\mathbb{R})](https://konrad.burnik.org/wordpress/wp-content/ql-cache/quicklatex.com-5791b83f990fe4853f18a333a6ddcad3_l3.png) . For each
. For each 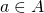 we have
we have 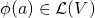 . Since
. Since 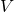 is
is 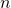 -dimensional, we have and ordered basis
-dimensional, we have and ordered basis 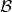 and
and ![Rendered by QuickLaTeX.com [\phi(a)]_\mathcal{B} \in M_n(\mathbb{R})](https://konrad.burnik.org/wordpress/wp-content/ql-cache/quicklatex.com-cef0b0493a1932fe8a0bc57934c16081_l3.png) . A matrix representation of
. A matrix representation of 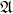 with respect to
with respect to 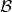 } is a map
} is a map 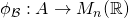 such that
such that ![Rendered by QuickLaTeX.com \phi_\mathcal{B}(a) = [\phi(a)]_\mathcal{B}](https://konrad.burnik.org/wordpress/wp-content/ql-cache/quicklatex.com-0c7f8d77f75011bb6e57fc5e5e1f4d25_l3.png) for all
for all 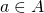 . Further, we have
. Further, we have 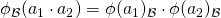 for all
for all 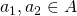 . These are all well known notions from representation theory, for further information, one can consult one of the standard textbooks, for example see [3].
. These are all well known notions from representation theory, for further information, one can consult one of the standard textbooks, for example see [3].
Algebra of split-complex numbers
Let 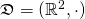 , where
, where 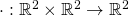 is given by
is given by
(1) 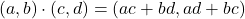
for all
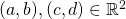
. It is straightforward to verify that
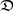
is
an algebra. This is the well known algebra of
split-complex numbers. The split-complex numbers are also sometimes known as
hyperbolic numbers.
Similarly as for the complex numbers, each real number
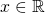
can be identified with the pair
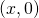
.
With this correspondence, the pair
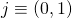
has the property
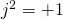
and
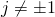
. Due to this property,
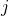
is called the
hyperbolic unit.
Since
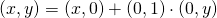
, in the following we shall denote a pair
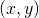
simply with
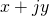
. The
conjugate of
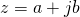
is defined as
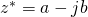
.
For a hyperbolic number 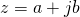 we define the real part as
we define the real part as 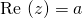 and hyperbolic part as
and hyperbolic part as 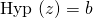 .
.
For the module we set 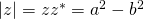 and we have
and we have 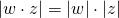 for all
for all 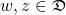 .
.
For an extensive overview of the theory of hyperbolic numbers as well of their usefulness in Physics one can check the literature, for example [2]. For the rest of this blog post, we shall refer to these numbers as split-complex numbers.
Centrosymmetric representation of split-complex matrices
By 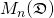 we denote the set of all
we denote the set of all 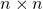 split-complex matrices i.e. matrices in which entries are split-complex numbers. Note that
split-complex matrices i.e. matrices in which entries are split-complex numbers. Note that 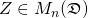 if and only if there exist
if and only if there exist 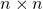 real matrices
real matrices 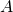 ,
, 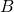 such that
such that 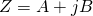 . If
. If 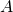 is a matrix then its transpose is defined as
is a matrix then its transpose is defined as 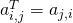 for all
for all 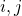 and is denoted with
and is denoted with 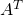 . In the following we denote by
. In the following we denote by 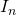 the
the 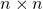 identity matrix and by
identity matrix and by 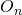 the
the 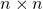 zero matrix. Let
zero matrix. Let 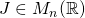 be defined as
be defined as 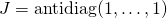 for each
for each 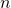 . Note that
. Note that 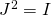 . A matrix
. A matrix 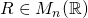 is upper-triangular if
is upper-triangular if 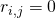 for all
for all 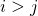 .
.
A real matrix 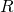 is centrosymmetric if
is centrosymmetric if 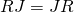 . An overview of centrosymmetric matrices can be found in [4]. We denote by
. An overview of centrosymmetric matrices can be found in [4]. We denote by 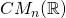 the set of all
the set of all 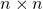 centrosymmetric real matrices.
centrosymmetric real matrices.
For the algebra 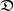 of split-complex numbers the well-known matrix representation
of split-complex numbers the well-known matrix representation 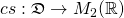 with respect to
with respect to 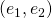 is given by
is given by
(2) 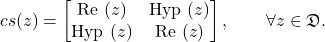
It is straightforward to check that for all
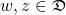
we have
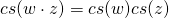
.
Further, on the vector space 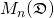 there is a natural multiplication operation
there is a natural multiplication operation 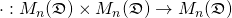 given by
given by
(3) 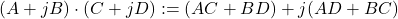
for all
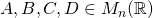
. It is easy to verify that
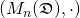
is an algebra. In the following we refer to this algebra as the
algebra of split-complex (square) matrices and denote it with
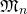
.
Note that in the following whenever we have two matrices 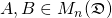 , their product shall explicitly be written with a dot '
, their product shall explicitly be written with a dot ' ', e.g.
', e.g.  to indicate multiplication defined in (3). Otherwise, if
to indicate multiplication defined in (3). Otherwise, if 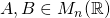 we simply write
we simply write 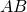 .
.
To state and prove our main result, we shall need the following well known characterization of centrosymmetric matrices.
Proposition 1:
Let 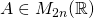 . Then
. Then 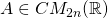 if and only if there exist
if and only if there exist 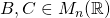 such that
such that
(4) 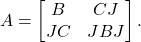
Proof:
Suppose
![Rendered by QuickLaTeX.com \[A =\begin{bmatrix}X & Y \\W & Z\end{bmatrix}.\]](https://konrad.burnik.org/wordpress/wp-content/ql-cache/quicklatex.com-dfc22a1c4d521ab6264a5e940d168b8b_l3.png)
Since
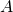
is centrosymmetric, we have
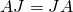
, or equivalently, in block-form
*** QuickLaTeX cannot compile formula:
\[\begin{bmatrix}\ & J \\J & \\end{bmatrix}\begin{bmatrix}X & Y \\W & Z\end{bmatrix} =\begin{bmatrix}X & Y \\W & Z\end{bmatrix}\begin{bmatrix}\ & J \\J & \\end{bmatrix}\]
*** Error message:
\begin{bmatrix} on input line 17 ended by \end{equation*}.
leading text: ...begin{bmatrix}\ & J \\J & \\end{bmatrix}\]
Missing $ inserted.
leading text: ...begin{bmatrix}\ & J \\J & \\end{bmatrix}\]
Missing } inserted.
leading text: ...begin{bmatrix}\ & J \\J & \\end{bmatrix}\]
Missing \cr inserted.
leading text: ...begin{bmatrix}\ & J \\J & \\end{bmatrix}\]
Missing $ inserted.
leading text: ...begin{bmatrix}\ & J \\J & \\end{bmatrix}\]
Missing } inserted.
leading text: ...begin{bmatrix}\ & J \\J & \\end{bmatrix}\]
Missing \right. inserted.
leading text: ...begin{bmatrix}\ & J \\J & \\end{bmatrix}\]
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
This is equivalent to
![Rendered by QuickLaTeX.com \[\begin{bmatrix}JW & JZ \\JX & JY\\end{bmatrix} =\begin{bmatrix}YJ & XJ \\ZJ & WJ\end{bmatrix}\]](https://konrad.burnik.org/wordpress/wp-content/ql-cache/quicklatex.com-dd5627f494d4bca7581085523a98716c_l3.png)
We now have
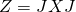
and
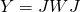
, so
![Rendered by QuickLaTeX.com \[A = \begin{bmatrix}X & JWJ \\W & JXJ\end{bmatrix}\]](https://konrad.burnik.org/wordpress/wp-content/ql-cache/quicklatex.com-7c3957443d30be0edce1f4d5805ced92_l3.png)
Now, by choosing
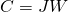
and
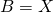
and from the fact
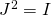
it follows that
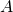
has the form (4).
Conversely, suppose 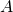 has the form (4). It can easily be shown by block-matrix multiplication that
has the form (4). It can easily be shown by block-matrix multiplication that 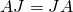 , hence
, hence 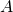 is centrosymmetric.
is centrosymmetric.
QED.
The map 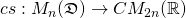 defined as
defined as
(5) 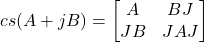
is a matrix representation of
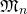
. We call the representation
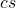
the
standard centrosymmetric matrix representation of
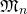
.
Proof:
Let 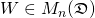 and
and 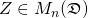 be such that
be such that 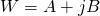 and
and 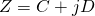 .
.
We now have
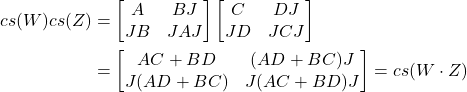
which proves the claim.
QED.
Proposition.
Let 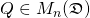 . Then
. Then 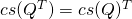 .
.
Proof.
Let 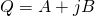 . Then
. Then
![Rendered by QuickLaTeX.com \[{cs}(Q^T) = {cs}(A^T + jB^T) = \begin{bmatrix}A^T & B^T J \\J B^T & J A^T J\end{bmatrix}.\]](https://konrad.burnik.org/wordpress/wp-content/ql-cache/quicklatex.com-50052d6274db4c924f8f8c3e0721d654_l3.png)
On the other hand, keeping in mind that
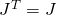
we have
![Rendered by QuickLaTeX.com \[{cs}(Q)^T = \begin{bmatrix}A & B J \\J B & JAJ\end{bmatrix}^T =\begin{bmatrix}A^T & (JB)^T \\(BJ)^T & (JAJ)^T\end{bmatrix}= \begin{bmatrix}A^T & B^T J \\J B^T & J A^T J\end{bmatrix}.\]](https://konrad.burnik.org/wordpress/wp-content/ql-cache/quicklatex.com-9714f4b56d03557826eb2b0e6f887b47_l3.png)
Hence,
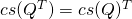
.
QED.
Proposition.
The map 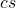 is a bijection.
is a bijection.
Proof.
Injectivity. Let 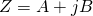 and
and 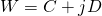 and
and 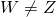 . From this,
. From this,
it follows that 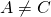 or
or 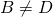 . Assume that
. Assume that 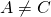 . Then
. Then

Since
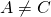
we have
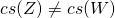
. Let now
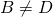
and assume that
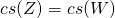
. Then from
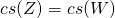
it follows
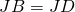
. Now multiplying
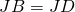
with
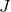
from the left implies
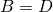
, which is a contradiction.
We conclude that
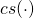
is injective.
Surjectivity. Let 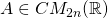 . By proposition 1 we can find matrices
. By proposition 1 we can find matrices 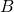 and
and 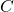 such that (4) holds. But then
such that (4) holds. But then 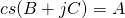 and since
and since 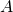 was arbitrary, we conclude that
was arbitrary, we conclude that 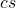 is surjective.
is surjective.
Now, injectivity and surjectivity of 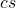 imply by definition that
imply by definition that 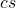 is a bijection.
is a bijection.
QED.
Correspondence of QR decompositions
Definition:
Let 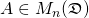 . A pair
. A pair 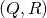 with
with 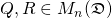 is a QR decomposition of
is a QR decomposition of 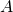 over
over 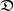 if the following holds:
if the following holds:
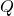 is orthogonal, i.e.
is orthogonal, i.e. 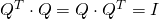 ,
,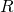 is upper-triangular,
is upper-triangular,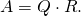
The notion of a 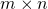 double-cone matrix was introduced by the author in [1].
double-cone matrix was introduced by the author in [1].
Here we state the definition in block-form for the case of 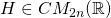 .
.
Definition:
Let 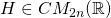 . Then
. Then 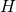 is a double-cone matrix iff there exist
is a double-cone matrix iff there exist 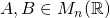 both upper-triangular such that
both upper-triangular such that
![Rendered by QuickLaTeX.com \[H = \begin{bmatrix}A & BJ \\JB & JAJ\end{bmatrix}.\]](https://konrad.burnik.org/wordpress/wp-content/ql-cache/quicklatex.com-808405c728b3915d63f5080e9576518b_l3.png)
Definition:
Let 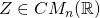 . A pair
. A pair 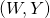 , with
, with 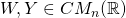 is a centrosymmetric QR decomposition of
is a centrosymmetric QR decomposition of 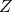 if the following holds:
if the following holds:
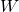 is orthogonal matrix,
is orthogonal matrix,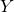 is double-cone matrix,
is double-cone matrix,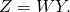
The algorithm to obtain an approximation of a centrosymmetric QR decomposition of a given centrosymmetric matrix 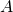 was given in [1].
was given in [1].
The following theorem provides one interpretation of the centrosymmetric QR decomposition, in the case of square centrosymmetric matrices of even order by establishing the equivalence of their centrosymmetric QR decomposition with the QR decomposition of the corresponding split-complex matrix.
Theorem 1 (QR decomposition correspondence):
Let 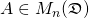 . Then
. Then 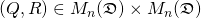 is a QR decomposition of
is a QR decomposition of 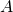 if and only if
if and only if
![Rendered by QuickLaTeX.com \[(\CsEmb{Q}, \CsEmb{R}) \in \CsMat{2n} \times \CsMat{2n}\]](https://konrad.burnik.org/wordpress/wp-content/ql-cache/quicklatex.com-e9a458e3f996c705150a04da9762d369_l3.png)
is a centrosymmetric QR decomposition of
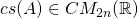
.
Proof.
Let 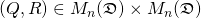 be a QR decomposition of
be a QR decomposition of 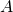 .
.
Let 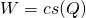 and
and 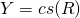 . We have
. We have

Since
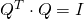
it follows that
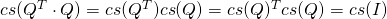
.
From this we have
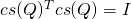
i.e.
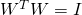
hence
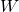
is orthogonal. Since
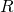
is upper-triangular and
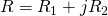
, then by definition we have that both
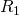
and
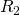
are upper-triangular. Further,
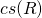
is centrosymmetric by definition. From this it follows that
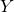
is centrosymmetric double-cone.
Finally, we have
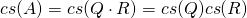
. Hence,
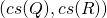
is
a centrosymmetric QR decomposition of
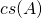
.
Conversely, let 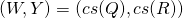 . If
. If 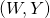 is a centrosymmetric QR decomposition of
is a centrosymmetric QR decomposition of 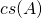 then
then 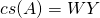 where
where 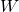 is centrosymmetric and orthogonal and
is centrosymmetric and orthogonal and 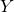 is a double-cone matrix.
is a double-cone matrix.
From the fact that 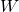 is centrosymmetric we have (by Proposition 1) that
is centrosymmetric we have (by Proposition 1) that
![Rendered by QuickLaTeX.com \[W = \begin{bmatrix}W_1 & W_2 J \\J W_2 & J W_1 J\end{bmatrix}\]](https://konrad.burnik.org/wordpress/wp-content/ql-cache/quicklatex.com-c10ff9bad6cc022b85b4befe7f99a024_l3.png)
Now the property of
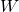
being orthogonal i.e. the condition
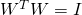
implies
(6) 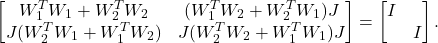
On the other hand, we have
(7) 
First we prove that
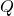
is orthogonal. From (6) we obtain
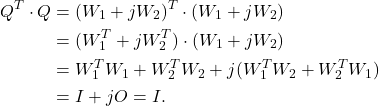
The matrix
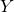
is centrosymmetric and double-cone which implies
![Rendered by QuickLaTeX.com \[Y = \begin{bmatrix}Y_1 & Y_2 J \\J Y_2 & J Y_1 J\end{bmatrix}\]](https://konrad.burnik.org/wordpress/wp-content/ql-cache/quicklatex.com-5788a9be2737c3666186cb5481c37365_l3.png)
where both
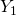
and
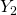
are upper-triangular. This now implies that
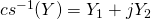
is upper-triangular.
Finally, let us prove that 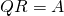 . We have
. We have
![Rendered by QuickLaTeX.com \[Q \cdot R = {cs}^{-1} (W) {cs}^{-1} (Y) = {cs}^{-1}(WY) = {cs}^{-1}(\CsEmb{A}) = A.\]](https://konrad.burnik.org/wordpress/wp-content/ql-cache/quicklatex.com-dd022056b2f5c502b64e158d2a87d15e_l3.png)
We conclude that
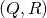
is a QR decomposition of
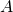
.
QED.
Example:
Let
![Rendered by QuickLaTeX.com \[A = \begin{bmatrix}1 + 2j & 2 + 3j \\3 + 4j & 4 + 5j\end{bmatrix}.\]](https://konrad.burnik.org/wordpress/wp-content/ql-cache/quicklatex.com-db6205a4ba7d1af37703a787ba0df9c9_l3.png)
Note that
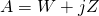
where
(8) 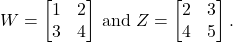
We have
![Rendered by QuickLaTeX.com \[{cs}(A) = {cs}(W + jZ) = \begin{bmatrix}W & ZJ \\JZ & JWJ\end{bmatrix}= \begin{bmatrix}1 & 2 & 3 & 2 \\3 & 4 & 5 & 4 \\4 & 5 & 4 & 3 \\2 & 3 & 2 & 1\end{bmatrix}\]](https://konrad.burnik.org/wordpress/wp-content/ql-cache/quicklatex.com-1c69ab9d656b5f8fe677e72f6445a893_l3.png)
By applying the
algorithm from [1] to
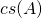
we obtain the approximations:
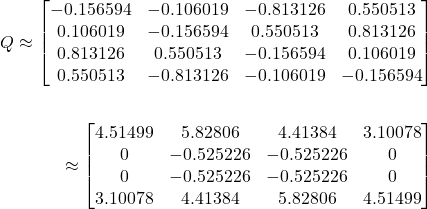
Applying 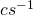 to
to 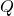 and
and 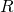 yields:
yields:
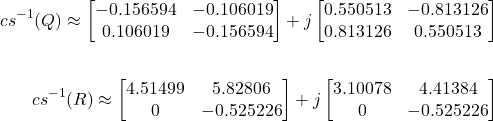
with
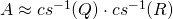
. Now, from Theorem 1 we conclude that
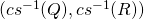
is an approximation of a QR decomposition of
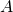
.
Conclusion
We introduced the standard centrosymmetric representation 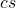 for split-complex matrices. Using this representation we proved that a QR decomposition of a square split-complex matrix
for split-complex matrices. Using this representation we proved that a QR decomposition of a square split-complex matrix 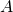 can be obtained by calculating the centrosymmetric QR decomposition introduced by the author in [1] of its centrosymmetric matrix representation
can be obtained by calculating the centrosymmetric QR decomposition introduced by the author in [1] of its centrosymmetric matrix representation 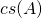 .
.
References
- Burnik, Konrad. A structure-preserving QR factorization for centrosymmetric real matrices,
Linear Algebra and its Applications 484(2015) 356 - 378
- Catoni, Francesco and Boccaletti, Dino and Cannata, Roberto and Catoni, Vincenzo and Zampeti, Paolo, Hyperbolic Numbers. Geometry of Minkowski Space-Time Springer Berlin Heidelberg Berlin, Heidelberg, (2011) 3–23 ISBN: 978-3-642-17977-8
- Curtis, Charles W.; Reiner, Irving. Representation Theory of Finite Groups and Associative Algebras, John Wiley & Sons (Reedition2006 by AMS Bookstore), (1962) ISBN 978-0-470-18975
- James R. Weaver. Centrosymmetric (Cross-Symmetric) Matrices,Their Basic Properties, Eigenvalues, and Eigenvectors, The American Mathematical Monthly, Mathematical Association of America, (1985) 10-92, 711–717 ISSN: 00029890, 19300972 doi:10.2307/2323222
QR_decomposition_of_split_complex_matric
Copyright © 2018, Konrad Burnik
![]() such that it has an infinite metric base
such that it has an infinite metric base ![]() with the following properties:
with the following properties: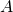 is not dense;
is not dense;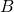 of
of 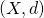 we have
we have 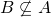 ?"
?"![]() be defined as
be defined as![]()
![]() . Then
. Then ![]() is a metric on
is a metric on ![]() , denoted by
, denoted by ![]() and
and ![]() is a metric space.
is a metric space.![]() and the integer lattice
and the integer lattice ![]() as the candidate for such a set. Here I will explain why this set is a good candidate.
as the candidate for such a set. Here I will explain why this set is a good candidate.![]() . Then
. Then ![]() is a countable set, which is not dense in
is a countable set, which is not dense in ![]() which can be seen by taking for example
which can be seen by taking for example ![]() and
and ![]() then
then ![]() . By [1] the space
. By [1] the space ![]() does not have a finite metric base, therefore
does not have a finite metric base, therefore ![]() itself can not contain a finite metric base. What is left to prove is that
itself can not contain a finite metric base. What is left to prove is that ![]() is a metric base for
is a metric base for ![]() . The rest of this blog post is concerned with proving this fact.
. The rest of this blog post is concerned with proving this fact.![]() such that either
such that either ![]() ,
, ![]() or
or ![]() ,
, ![]() Let
Let ![]() . Then
. Then ![]() is a metric base for
is a metric base for ![]() .
.![]() . My conjecture is that this also gives a complete characterisation of finite metric bases for
. My conjecture is that this also gives a complete characterisation of finite metric bases for ![]() however, this is a topic for another blog post. For now, it seems that the result stated in Proposition 1 coincides with some parts of results from [1] and as such will be sufficient for our needs.
however, this is a topic for another blog post. For now, it seems that the result stated in Proposition 1 coincides with some parts of results from [1] and as such will be sufficient for our needs.![]() and
and ![]() be metric spaces. If
be metric spaces. If ![]() is a metric base for
is a metric base for ![]() and
and ![]() is an onto mapping such that there exists
is an onto mapping such that there exists ![]() with the property
with the property![]()
![]() , then
, then ![]() is a metric base for
is a metric base for ![]() .
.![]() where
where ![]() by using the known result of Proposition 1 and finding a suitable map
by using the known result of Proposition 1 and finding a suitable map ![]() .
.![]() be a metric base for
be a metric base for ![]() . Let
. Let ![]() where
where ![]() be defined as
be defined as![]()
![]() . Then
. Then ![]() is a metric base for
is a metric base for ![]() .
.![]() it is easy to verify that
it is easy to verify that ![]() defined in Proposition 3 satisfies the property of
defined in Proposition 3 satisfies the property of ![]() from Proposition 2.
from Proposition 2.![]() is indeed a metric base for
is indeed a metric base for ![]() .
.![]() is a metric base for
is a metric base for ![]() .
.![]() . Let
. Let ![]() and assume that
and assume that![]()
![]() .
.![]() such that
such that ![]() and
and ![]() . Namely, we can take for example
. Namely, we can take for example ![]() such that
such that ![]() and set
and set ![]() . Now set
. Now set ![]() and
and ![]() .
.![]() are a metric base for
are a metric base for ![]() . By Proposition 3 there is a map
. By Proposition 3 there is a map ![]() such that
such that ![]() is a metric base for
is a metric base for ![]() . Since
. Since ![]() , then
, then ![]() for all
for all ![]() implies
implies ![]() .
.![]() is a metric base for
is a metric base for ![]() .
.![Rendered by QuickLaTeX.com \[\begin{bmatrix}JW & JZ \\JX & JY\\end{bmatrix} =\begin{bmatrix}YJ & XJ \\ZJ & WJ\end{bmatrix}\]](https://konrad.burnik.org/wordpress/wp-content/ql-cache/quicklatex.com-dd5627f494d4bca7581085523a98716c_l3.png)
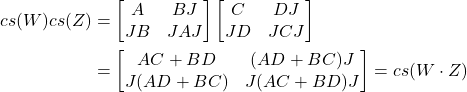
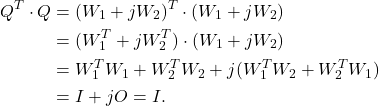
![Rendered by QuickLaTeX.com \[{cs}(A) = {cs}(W + jZ) = \begin{bmatrix}W & ZJ \\JZ & JWJ\end{bmatrix}= \begin{bmatrix}1 & 2 & 3 & 2 \\3 & 4 & 5 & 4 \\4 & 5 & 4 & 3 \\2 & 3 & 2 & 1\end{bmatrix}\]](https://konrad.burnik.org/wordpress/wp-content/ql-cache/quicklatex.com-1c69ab9d656b5f8fe677e72f6445a893_l3.png)

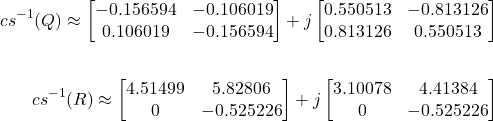






![Rendered by QuickLaTeX.com \[\chi_S(x) =\begin{cases} 1, & x \in S \\ 0, & x \not \in S \end{cases}\]](https://konrad.burnik.org/wordpress/wp-content/ql-cache/quicklatex.com-064bd0cca97592aa71745aad2444c6ab_l3.png)