#####################################################################
#
# Implementing the notion of Computable Set in the euclidean plane 
#
# Every weakly computable set in the euclidean plane is a set 
# of zeroes of some a computable function.
#
# Konrad Burnik, June 2017.
#
#####################################################################

from math import *
from decimal import *
import matplotlib.pyplot as plt

class ComputableSet:
    '''A computable subset of the euclidean plane is given by its computable function representing it.'''
    def f(self, x, y):
        '''A function whose zeroes represent this computable set. 
           For example: def f(x, y): return x**2 + y**2 - 1 has zeroes which represents a unit circle.
        '''
        raise Exception("Not implemented!")
    
    def points(self, k):
        return [(x/2**k, y/2**k) 
                        for y in range(-2**k, 2**k + 1) 
                        for x in range(-2**k, 2**k + 1) 
                        if Decimal(-1) / Decimal(2**k) < self.f(Decimal(x)/Decimal(2**k), Decimal(y)/Decimal(2**k)) < Decimal(1) / Decimal(2**k)]  class Circle(ComputableSet):
    def f(self, x, y):
        return x**2 + y**2 - Decimal(1/2)
class EllipticCurve(ComputableSet):
    def f(self, x, y):
        return x**2 + y**3 - Decimal(1/2)

def plot_set(s, k):
    points = s.points(k)
    x = list(map(lambda x : x[0], points))
    y = list(map(lambda x : x[1], points))

    plt.plot(x, y, 'ro')
    plt.show()

class Circle(ComputableSet):
    def f(self, x, y):
        return x**2 + y**2 - Decimal(1/2)

class EllipticCurve(ComputableSet):
    def f(self, x, y):
        return x**2 + y**3 - Decimal(1/2)

class ComputableSetUnion(ComputableSet):
    def __init__(self):
        self.A = ComputableSet()
        self.B = ComputableSet()
        
    def f(self, x, y):
        return self.A.f(x, y) * self.B.f(x, y)

+1

0

What is Computable analysis anyway?

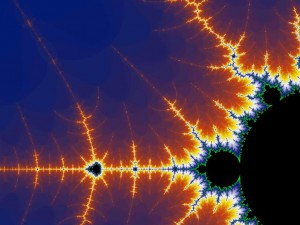
Roger Penrose in his book "The emperors new Mind" asked an interesting question regarding the Mandelbrot set: "Is the Mandelbrot set recursive?" The term "recursive" is an old name for "computable" and has nothing to do with recursion in programming.

The Mandelbrot Set (zoomed in)

Classical computability theory (also known as recursion theory) is a branch of mathematical logic that deals with studying what functions are computable. Computable analysis is in some sense an extension of this theory. It is a branch of mathematics that applies computability theory to problems in mathematical analysis. It is concerned with questions of effectivity in analysis and its main goal is to find what parts of analysis can be described by an algorithmic procedure, one of the basic questions being what functions are computable? (note the domain and codomain are now the reals).

Computable reals

Suppose we take a real number . Is computable? What do we mean by being computable? If we can find an algorithm that calculates for each input a rational approximation of ; and such that the sequence "converges fast" to then we say that is a computable real. More precisely, a real number is computable iff there exists a computable function such that for each . For example, every rational number is computable. The famous number is computable, and in our previous post we proved that is computable. It turns out that the set of computable reals, denoted by is a field with respect to addition and multiplication. But there exist real numbers which are not computable. This is easy to see as there is only a countable number of computable functions , and since we know that is uncountable, so we have more real numbers than we have possible algorithms, we conclude that there must be a real number that is not computable. One example of an uncomputable real is the limit of a Specker sequence. And one other interesting one is the Chaitin constant. In fact, if we take any recursively enumerable but non-recursive set , then the number is an example of a real number which is not computable.

Computable sequences of reals

If we have a sequence of computable reals   (and hence a sequence of algorithms) we may ask if this sequence is computable i.e. is there a single algorithm that describes the whole sequence? If there exists a computable function  such that  

for each then we say that is a computable sequence. We have seen that each rational number is computable, but this is not true for sequences of rational numbers! One example of a sequence that has each term computable but it is not uniformly computable is the following:

Computable real functions

Real functions which are a main object of study in analysis can be studied in this computability setting, a function is computable iff  

1. it maps computable sequences to computable sequences i.e. 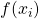is computable for every computable sequence ;
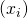2. it is effectively uniformly continous i.e. if there exists a computable sequence thatdescribes the modulus of continuity of .

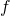The fundamental theorem of computable analysis is that every computable real function is continuous.

There is also a notion of computability for the process of integration, derivation, solving partial differential equations, etc. and we shall look into that topic in another post.

Computable subsets of the Euclidean space

Unit circle approximated with dyadic points

Next, let's look at the subsets of the euclidean space and ask a simple question: what subsets are computable? First, note that saying is computable iff its indicator function

is computable is not a useful definition since the indicator function is not continous except when or . A subset of is computable iff the function   defined as is a computable function. For example, take the unit circle in .  

. The distance function is

  These are just some basic definitions and facts, but also interesting questions are studied in computable analysis like for example what mappings preserve computability of objects?  Is for example the Mandelbrot set computable? What about Julia Sets? For them, there are nice results presented in the book "Computability of Julia Sets" by Braverman and Yampolsky. Although Julia Sets have been thoroughly researched in the book, for the Mandelbrot set we still don't know the answer.

Basically for anything we do in analysis (finding derivatives, integration, finding roots, solving PDEs ...) we may ask: "Is it computable?" and that is a topic for another post.

(to be continued)

Copyright © 2014, Konrad Burnik

+1

0

The other day I was thinking about approximating in terms of segments of size for , The question I was interested was "What is the least number of segments of length that we need to cross over starting from zero?" and one particular sequence of integers I came up with was this:

Sadly, at the time of writing this post the Online Encyclopedia of Integer Sequences did not return anything for this sequence.

The sequence represents the numerators for dyadic rationals which approximate within precision (within k-bits of precision), but is this sequence computable? In what follows I assume that the reader is familiar with the basic definitions of mu-recursive functions.

It turns out that our sequence can be described by a recursive function

for all .

The idea of the function is that for each it outputs the number of segments that fit into plus one.

Since for each , the value is the smallest integer such that we have

for each .

From this we obtain the error bound .

Approximation of within precision can be "represented" by a natural number . To get the actual approximation by a dyadic rational just divide by but what we want is to avoid division. We want to calculate only with natural numbers!

Implementation

The function f has a straightforward (although inefficient) implementation in Python.

def calcSqrt2Segments(k):
    n = 0
    while(n*n <= 2**(2*k+1)):
        n = n + 1
    return n

This is in fact terribly inefficient, but in computability theory efficiency is not the goal, the goal is usually to prove that something is uncomputable even if you have all the resources of time and space at your disposal. Nevertheless, here is a slightly better version we get if we notice that the next term is about twice as large as with a small correction.

def calcSqrt2segmentsRec(k):
    if k == 0:
        return 2
    else:
        res = 2*calcSqrt2segmentsRec(k-1) - 1
        if res*res <= 2**(2*k+1):
           res = res + 1
        return res

This of course suffers from stack overflow problems, so memoization is a natural remedy.

def calcSqrt2segmentsMemo(k):
    m = dict()
    m[0] = 2
    for j in range(1, k+1):
        m[j] = 2*m[j-1] - 1
        if m[j]*m[j] <= 2**(2*j+1):
            m[j] = m[j] + 1
    return m[k]

Memoization can use-up memory and we can do  better. We don't need to memorize the whole sequence up to k to calculate we only need the value .

def calcSqrt2segmentsBest(k):
    m = 2
    for j in range(1, k+1):
        m = 2*m - 1
        if m*m <= 2**(2*j+1):
            m = m + 1
    return m

After defining a simple timing function and testing our memoization and "best" version we see that the best version is not so good in terms of running time when compared with memoization, they are both approximately about the same in terms of speed (the times are in seconds):

>>> timing(calcSqrt2segmentsMemo, 10000)
0.6640379428863525
>>> timing(calcSqrt2segmentsBest, 10000)
0.6430368423461914
>>> timing(calcSqrt2segmentsMemo, 20000)
3.3311898708343506
>>> timing(calcSqrt2segmentsBest, 20000)
3.3061890602111816
>>> timing(calcSqrt2segmentsMemo, 30000)
8.899508953094482
>>> timing(calcSqrt2segmentsBest, 30000)
8.848505973815918
>>> timing(calcSqrt2segmentsMemo, 50000)
30.04171895980835
>>> timing(calcSqrt2segmentsBest, 50000)
29.96371293067932
>>> timing(calcSqrt2segmentsMemo, 100000)
164.99343705177307
>>> timing(calcSqrt2segmentsBest, 100000)
168.6026430130005

Neverteless, we can use our "best" program to calculate to arbritrary number of decimal places (in base 10). First, we need to determine how many bits are sufficient to calculate to decimal places in base 10. Simple calculation yields:

In Python we need a helper function that calculates this bound that avoids the nasty log and ceiling functions, so here it is:

def calcNumDigits(n):
    res = 1
    for j in range(2, n+1): 
        if( j%3 == 0 or j%3 == 1 ):
          res = res + 3
        else:
          res = res + 4
    return res

At last, calculating to arbritrary precision is done with this simple code below, returning a String with the digits of in base 10. Note once more, that all this calculation is done only with the natural numbers and here we are using Python's powerful implementation of arithmetic with arbritrary long integers (which is not as nicely supported for decimals at least at the time of writing this post).

Note also, that instead of dividing by we are multiplying it with to get a natural number with all of it's digits being an approximation of with k bits of precision. This natural number we are then converting to a string, inserting a decimal point '.' and returning this as our result. So, here is the code:

def calcSqrt2(n):
    k = calcNumDigits(n)
    res = str(5**k * calcSqrt2segmentsBest(k))
    return res[0:1] + '.' + res[1:n]

Running it gives us nice results:

>>> calcSqrt2(30)
'1.41421356237309504880168872421'
>>> calcSqrt2(300)
'1.41421356237309504880168872420969807856967187537694807317667973799073247846210703885038753432764157273501384623091229702492483605585073721264412149709993583141322266592750559275579995050115278206057147010955997160597027453459686201472851741864088919860955232923048430871432145083976260362799525140799'
>>> calcSqrt2(3000)
'1.41421356237309504880168872420969807856967187537694807317667973799073247846210703885038753432764157273501384623091229702492483605585073721264412149709993583141322266592750559275579995050115278206057147010955997160597027453459686201472851741864088919860955232923048430871432145083976260362799525140798968725339654633180882964062061525835239505474575028775996172983557522033753185701135437460340849884716038689997069900481503054402779031645424782306849293691862158057846311159666871301301561856898723723528850926486124949771542183342042856860601468247207714358548741556570696776537202264854470158588016207584749226572260020855844665214583988939443709265918003113882464681570826301005948587040031864803421948972782906410450726368813137398552561173220402450912277002269411275736272804957381089675040183698683684507257993647290607629969413804756548237289971803268024744206292691248590521810044598421505911202494413417285314781058036033710773091828693147101711116839165817268894197587165821521282295184884720896946338628915628827659526351405422676532396946175112916024087155101351504553812875600526314680171274026539694702403005174953188629256313851881634780015693691768818523786840522878376293892143006558695686859645951555016447245098368960368873231143894155766510408839142923381132060524336294853170499157717562285497414389991880217624309652065642118273167262575395947172559346372386322614827426222086711558395999265211762526989175409881593486400834570851814722318142040704265090565323333984364578657967965192672923998753666172159825788602633636178274959942194037777536814262177387991945513972312740668983299898953867288228563786977496625199665835257761989393228453447356947949629521688914854925389047558288345260965240965428893945386466257449275563819644103169798330618520193793849400571563337205480685405758679996701213722394758214263065851322174088323829472876173936474678374319600015921888073478576172522118674904249773669292073110963697216089337086611567345853348332952546758516447107578486024636008344491148185876555542864551233142199263113325179706084365597043528564100879185007603610091594656706768836055717400767569050961367194013249356052401859991050621081635977264313806054670102935699710424251057817495310572559349844511269227803449135066375687477602831628296055324224269575345290288387684464291732827708883180870253398523381227499908123718925407264753678503048215918018861671089728692292011975998807038185433325364602110822992792930728717807998880991767417741089830608003263118164279882311715436386966170299993416161487868601804550555398691311518601038637532500455818604480407502411951843056745336836136745973744239885532851793089603738989151731958741344288178421250219169518755934443873961893145499999061075870490902608835176362247497578588583680374579311573398020999866221869499225959132764236194105921003280261498745665996888740679561673918595728886424734635858868644968223860069833526427990562831656139139425576490620651860216472630333629750756978706066068564981600927187092921531323682'

Note:
This can of course be generalized to calculating the square root of any number and of any order. This is an easy exercise for the reader.

Copyright © 2014, Konrad Burnik

+1

0