Introduction
In July 2018 professor Zvonko Iljazović and myself have attended the CCA 2018 conference and presented our joint work titled "Effective compactness and uniqueness of maximal computability structures". The original presentation can be found here.
Computability structures
In the following I will mention the elements of the theory of computability structures needed to state our main result. These notions are already well known, the main contributing articles for this theory that were used for our work are listed in the references.
Let 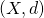 be a metric space and
be a metric space and 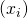 a sequence in
a sequence in 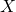 . We say
. We say 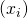 is an effective sequence in
is an effective sequence in 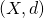 if the function
if the function 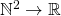
![Rendered by QuickLaTeX.com \[ (i,j) \mapsto d(x_i, x_j) \]](https://konrad.burnik.org/wordpress/wp-content/ql-cache/quicklatex.com-91f234d45af03859f15a89db670aa197_l3.png)
is recursive.
A finite sequence  is an effective finite sequence if
is an effective finite sequence if 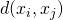 is a recursive real number for each
is a recursive real number for each 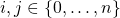 .
.
If 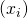 and
and 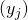 are sequences in
are sequences in 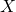 , we say
, we say 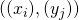 is an effective pair in
is an effective pair in 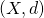 and write
and write 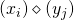 if the function
if the function 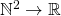 ,
,
![Rendered by QuickLaTeX.com \[ (i,j) \mapsto d(x_i, y_j) \]](https://konrad.burnik.org/wordpress/wp-content/ql-cache/quicklatex.com-ec79f8392d67775363f0fc6dbfddaf40_l3.png)
is recursive.
Let 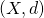 be a metric space and
be a metric space and 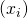 a sequence in
a sequence in 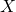 . A sequence
. A sequence 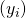 is computable w.r.t
is computable w.r.t 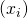 in
in 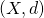 iff there exists a computable
iff there exists a computable 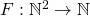 such that
such that
![Rendered by QuickLaTeX.com \[ d(y_i, x_{F(i, k)}) < 2^{-k} \]](https://konrad.burnik.org/wordpress/wp-content/ql-cache/quicklatex.com-76c2a60cd814845e0693dd4186a16b91_l3.png)
for all 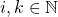 . We write
. We write 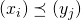 .
.
Let 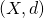 be a metric space. A set
be a metric space. A set 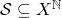 is a computability structure on
is a computability structure on 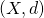 if the following holds:
if the following holds:
We say 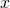 is a computable point in
is a computable point in 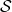 iff
iff 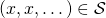 .
.
A computability structure 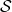 such that there exists a dense sequence
such that there exists a dense sequence 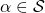 is called separable.
is called separable.
We say 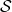 is a maximal computability structure on
is a maximal computability structure on 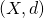 if there exists no computability structure
if there exists no computability structure 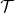 such that
such that 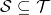 and
and 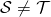 .
.
The main question
The main question we are asking and trying to answer is the following:
Question:Let 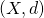 be a metric space. Let
be a metric space. Let 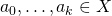 . Let
. Let 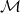 be a maximal computability structure in which
be a maximal computability structure in which 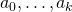 are computable. Under which conditions is such
are computable. Under which conditions is such  unique?
unique?
A known result for sub-spaces of the Euclidean space
Let  be a real vector space. Let
be a real vector space. Let 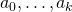 be vectors in
be vectors in 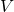 . We say that
. We say that 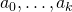 are geometrically independent points if
are geometrically independent points if  are linearly independent vectors.
are linearly independent vectors.
Let 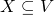 . The largest
. The largest 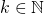 such that that there exist geometrically independent points
such that that there exist geometrically independent points 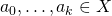 we call the affine dimension of
we call the affine dimension of 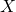 , and write
, and write 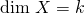 .
.
The following result from [1] already answers the main question in the case where 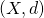 is a sub-space of the Euclidean space.
is a sub-space of the Euclidean space.
Theorem: Let 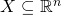 ,
, 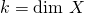 and
and 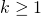 . If
. If 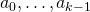 is a geometrically independent effective finite sequence on
is a geometrically independent effective finite sequence on 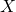 then there exists an unique maximal computability structure on
then there exists an unique maximal computability structure on 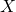 in which
in which 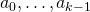 are computable points.
are computable points.
Main result for more general metric spaces
We wanted to introduce for general metric spaces a notion which will be a sort of replacement to the notion of geometric independence.
In the original presentation we used the term nice sequence. It turns out that this notion is a special case of the well-known notion of a metric base.
Let 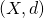 be a metric space. A subset
be a metric space. A subset 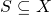 is called a metric base for
is called a metric base for 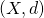 iff for all
iff for all 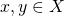 the following implication holds:
the following implication holds: 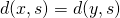 for all
for all 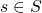 implies
implies 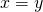 .
.
A metric space 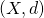 is said to be effectively compact if there exist an effective separating sequence
is said to be effectively compact if there exist an effective separating sequence 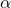 in
in 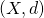 and a computable function
and a computable function 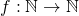 such that
such that
![Rendered by QuickLaTeX.com \[X=B(\alpha _{0} ,2^{-k})\cup \dots \cup B(\alpha _{f(k)},2^{-k})\]](https://konrad.burnik.org/wordpress/wp-content/ql-cache/quicklatex.com-5e70f2dc5b8fe0f958c67919c9d02c9a_l3.png)
for each 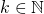 . It is known that if
. It is known that if 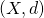 is effectively compact, then for each effective separating sequence
is effectively compact, then for each effective separating sequence 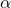 in
in 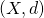 there exists such a computable function
there exists such a computable function 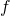 .
.
A metric base is exactly the notion we needed to obtain the following result, at least for effectively compact metric spaces.
Theorem: Let 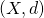 be an effectively compact metric space. Suppose
be an effectively compact metric space. Suppose 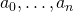 is a metric base in
is a metric base in 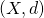 and suppose that there exists a separable computability structure
and suppose that there exists a separable computability structure 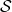 on
on 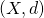 in which
in which 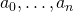 are computable points. Then
are computable points. Then 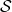 is a unique maximal computability structure on
is a unique maximal computability structure on 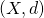 in which
in which 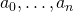 are computable points.
are computable points.
In fact, an even more general form of the theorem holds: the assumption of effective compactness of the space 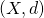 can be replaced with the assumption that
can be replaced with the assumption that 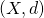 has compact closed balls and there exists
has compact closed balls and there exists 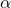 such that the computable metric space
such that the computable metric space 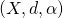 has the effective covering property.
has the effective covering property.
Proofs will be presented in our future up-coming publication.
References
- Zvonko Iljazović. Isometries and Computability Structures. Journal of Universal Computer Science, 16(18):2569--2596, 2010.
- Zvonko Iljazović and Lucija Validžić. Maximal computability structures. Bulletin of Symbolic Logic, 22(4):445--468, 2016.
- Alexander Melnikov. Computably isometric spaces. Journal of Symbolic Logic, 78:1055--1085, 2013.
- Marian Pour-El and Ian Richards. Computability in Analysis and Physics. Springer-Verlag, Berlin-Heielberg-New York, 1989.
- Klaus Weihrauch. Computable Analysis. Springer, Berlin, 2000.
- M. Yasugi, T. Mori and Y. Tsujji. Effective properties of sets and functions in metric spaces with computability structure. Theoretical Computer Science}, 219:467--486, 1999.
- M. Yasugi, T. Mori and Y. Tsujji. Computability structures on metric spaces. Combinatorics, Complexity and Logic Proc. DMTCS96 (D.S.~Bridges et al), Springer, Berlin}, 351--362, 1996.
Copyright © 2018, Konrad Burnik
