On April 22 and 23, I attended the 60th Netherlands Mathematical Congress. Two main topics I was particularly interested in were AI and Quantum Computing.

On April 22 and 23, I attended the 60th Netherlands Mathematical Congress. Two main topics I was particularly interested in were AI and Quantum Computing.

This week, during my vacation, I attended the Twenty-First International Conference on Computability and Complexity in Analysis. It was held at Swansea in Wales, UK. There I presented joint work with Zvonko Iljazović and Lucija Validžić. The title of the presentation was Computability of One-point Metric Bases. The slides can be found here.
Some photos from Swansea, including the Bay Campus can be found below.





On 8-12 July 2024, I attended online the Computability in Europe Conference 2024 held in Amsterdam. There were many interesting talks. Link to proceedings can be found here. Some of the recorded sessions can be found here.
The split-complex numbers are a special case of Clifford Algebra. This can be seen as follows. Let ![]() . Let
. Let ![]() with
with ![]() be a basis element of
be a basis element of ![]() . Then the Clifford Algebra
. Then the Clifford Algebra ![]() is defined as follows. The elements of the Clifford algebra are
is defined as follows. The elements of the Clifford algebra are ![]() . Setting the rule for the Clifford product
. Setting the rule for the Clifford product ![]() as
as
(1) ![]()
![]()
In my previous post, I showed that split-complex numbers can be used to speed up complex matrix multiplication.
In this post I will do a quick measurement on exactly how much faster is the new approach when compared to the naive implementation in practice. Since we are using 3 real matrix multiplications in the new approach as opposed to 4 in the naive approach we would expect up to 25% improvement in the runtime. We can easily implement and test this by using Python's NumPy library. In the following listing the hyperbolic_matrix_mult function is the new approach that uses split-complex numbers and complex_matrix_mult is the function implementing the naive complex matrix multiplication.
# matrix_mult.py
import numpy as np
def hyperbolic_matrix_mult(Z1, Z2, W1, W2):
X = 0.5 * (Z1 + Z2).dot(W1 + W2)
Y = 0.5 * (Z1 - Z2).dot(W1 - W2)
return X + Y - 2.0 * Z2.dot(W2), X - Y
def complex_matrix_mult(Z1, Z2, W1, W2):
return Z1.dot(W1) - Z2.dot(W2), Z1.dot(W2) + Z2.dot(W1)
I will be running the test on my MacBook laptop with the following specs:
Hardware Overview: Model Name: MacBook Pro Model Identifier: MacBookPro13,3 Processor Name: Quad-Core Intel Core i7 Processor Speed: 2,6 GHz Number of Processors: 1 Total Number of Cores: 4 L2 Cache (per Core): 256 KB L3 Cache: 6 MB Hyper-Threading Technology: Enabled Memory: 16 GB
The test will be as follows. First, we will generate four random real square matrices of order 10K. We use large matrices because we want the cost of multiplying the matrices to be the dominant factor in the runtime. Then, since the Jupyter notebook has nice features for timing the code, we can spin up a Jupyter notebook and perform the timing with the timeit command available as part of Jupyter. We will call timeit on both functions that will, by default, run the multiplication 7 times and calculate the mean and standard deviation of the collected run-times. This is all done in the following Jupyter Notebook snippet.
import numpy as np from matrix_mult import hyperbolic_matrix_mult, complex_matrix_mult n = 10000 A = np.random.rand(n, n) B = np.random.rand(n, n) C = np.random.rand(n, n) D = np.random.rand(n, n) %timeit hyperbolic_matrix_mult(A, B, C, D) %timeit complex_matrix_mult(A, B, C, D)
After running this for about 45 minutes on my machine, here are the results. The first line shows the runtime of the method using split-complex numbers and the second one is the runtime of the naive complex matrix implementation.
49.9 s ± 388 ms per loop (mean ± std. dev. of 7 runs, 1 loop each) 1 min 2s ± 985 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
Already from this simple test we see that the improvement in time of the new algorithm over naive complex multiplication is about 20% which is not bad. Stay tuned for more thourough testing in the next post.
Here is a nice application of split-complex numbers. Let ![]() and
and ![]() be complex matrices. Their product is defined as
be complex matrices. Their product is defined as
![]()
which requires 4 real matrix multiplications. Here I will show that we can do this with 3 real matrix multiplications by using split-complex numbers.
First, by taking split-complex matrices ![]() and
and ![]() and rewriting them in basis
and rewriting them in basis ![]() as follows
as follows
![]()
we have
![]()
which requires only 2 real matrix multiplications. This all follows from my previous post.
Let us now define
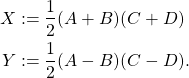
We have
![]()
But now, since
![]()
Finally, from this and the fact ![]() we have
we have
![]()
EDIT: A simple implementation of this approach can be found here.
The blog has migrated to a new server yesterday! It was running on an old server with outdated software since 2013. Special thanks to my brother Kristijan for jumping in with his expertise to do a quick setup and migration of the blog to the new and improved server!
Enjoy the speed and stability of the new blog!
A split-complex number is an algebraic expression of the form ![]() where
where ![]() and
and ![]() where
where ![]() . We can write a split-complex number simply as a pair of real numbers
. We can write a split-complex number simply as a pair of real numbers ![]() . Adding two split-complex numbers when represented as pairs is done component-wise. Hence, given
. Adding two split-complex numbers when represented as pairs is done component-wise. Hence, given ![]() and
and ![]() addition is defined as
addition is defined as
![]()
However, the product of two split-complex numbers is not defined component-wise since
![]()
One nice property of split-complex numbers is that we can change their representation in order to make multiplication component-wise as well.
Let
![]()
Now each hyperbolic number ![]() can uniquely be written in terms of
can uniquely be written in terms of![]() as follows.
as follows.
![]()
From here, the multiplication of two numbers ![]() and
and ![]() is now given component-wise by
is now given component-wise by
![]()
In this sense the transformed split-complex numbers algebraically behave just like two copies of real numbers since the algebraic operations are performed in each copy independently. More on this alternative representation of split-complex numbers in subsequent posts.
The CCA 2019 Conference was held in Zagreb, Croatia. I was one of the organizers as well as a presenter. I have presented joint work with Zvonko Iljazović.
Density_of_maximal_computability_structu