In Part 1 I posed the following question:
"Does there exist a metric space ![]() such that it has an infinite metric base
such that it has an infinite metric base ![]() with the following properties:
with the following properties:
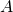 is not dense;
is not dense;- for all finite metric bases
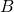 of
of 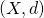 we have
we have 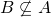 ?"
?"
Let ![]() be defined as
be defined as
![]()
for all ![]() . Then
. Then ![]() is a metric on
is a metric on ![]() , denoted by
, denoted by ![]() and
and ![]() is a metric space.
is a metric space.
After a brief chat with professor Zvonko Iljazović, he proposed the metric space ![]() and the integer lattice
and the integer lattice ![]() as the candidate for such a set. Here I will explain why this set is a good candidate.
as the candidate for such a set. Here I will explain why this set is a good candidate.
Let ![]() . Then
. Then ![]() is a countable set, which is not dense in
is a countable set, which is not dense in ![]() which can be seen by taking for example
which can be seen by taking for example ![]() and
and ![]() then
then ![]() . By [1] the space
. By [1] the space ![]() does not have a finite metric base, therefore
does not have a finite metric base, therefore ![]() itself can not contain a finite metric base. What is left to prove is that
itself can not contain a finite metric base. What is left to prove is that ![]() is a metric base for
is a metric base for ![]() . The rest of this blog post is concerned with proving this fact.
. The rest of this blog post is concerned with proving this fact.
First, note that the following result was mentioned briefly in our CCA 2018 presentation.
Proposition 1. Let ![]() such that either
such that either ![]() ,
, ![]() or
or ![]() ,
, ![]() Let
Let ![]() . Then
. Then ![]() is a metric base for
is a metric base for ![]() .
.
Interestingly enough, the article [1] already gives a complete characterisation of finite metric bases for squares in the digital plane for a couple of metrics including ![]() . My conjecture is that this also gives a complete characterisation of finite metric bases for
. My conjecture is that this also gives a complete characterisation of finite metric bases for ![]() however, this is a topic for another blog post. For now, it seems that the result stated in Proposition 1 coincides with some parts of results from [1] and as such will be sufficient for our needs.
however, this is a topic for another blog post. For now, it seems that the result stated in Proposition 1 coincides with some parts of results from [1] and as such will be sufficient for our needs.
We will also need the following claim, which is straightforward to establish.
Proposition 2. Let ![]() and
and ![]() be metric spaces. If
be metric spaces. If ![]() is a metric base for
is a metric base for ![]() and
and ![]() is an onto mapping such that there exists
is an onto mapping such that there exists ![]() with the property
with the property
![]()
for all ![]() , then
, then ![]() is a metric base for
is a metric base for ![]() .
.
By using Proposition 2 we can now easily find a metric base for an arbitrary square ![]() where
where ![]() by using the known result of Proposition 1 and finding a suitable map
by using the known result of Proposition 1 and finding a suitable map ![]() .
.
Proposition 3. Let ![]() be a metric base for
be a metric base for ![]() . Let
. Let ![]() where
where ![]() be defined as
be defined as
![]()
for all ![]() . Then
. Then ![]() is a metric base for
is a metric base for ![]() .
.
Note that by setting ![]() it is easy to verify that
it is easy to verify that ![]() defined in Proposition 3 satisfies the property of
defined in Proposition 3 satisfies the property of ![]() from Proposition 2.
from Proposition 2.
Finally, we now have everything we need to prove that ![]() is indeed a metric base for
is indeed a metric base for ![]() .
.
Proposition 4. ![]() is a metric base for
is a metric base for ![]() .
.
Proof.
Let ![]() . Let
. Let ![]() and assume that
and assume that
![]()
for all ![]() .
.
Note that we can always choose ![]() such that
such that ![]() and
and ![]() . Namely, we can take for example
. Namely, we can take for example ![]() such that
such that ![]() and set
and set ![]() . Now set
. Now set ![]() and
and ![]() .
.
From Proposition 1, it follows that any three corners of the square ![]() are a metric base for
are a metric base for ![]() . By Proposition 3 there is a map
. By Proposition 3 there is a map ![]() such that
such that ![]() is a metric base for
is a metric base for ![]() . Since
. Since ![]() , then
, then ![]() for all
for all ![]() implies
implies ![]() .
.
Therefore, ![]() is a metric base for
is a metric base for ![]() .
.
Q.E.D.
References
- Robert A. Melter and Ioan Tomescu "Metric Bases in Digital Geometry", Computer Vision, Graphics, and Image Processing Volume 25, Issue 1, January 1984, Pages 113-121 DOI: https://doi.org/10.1016/0734-189X(84)90051-3
- Konrad Burnik, Zvonko Iljazović, "Effective compactness and uniqueness of maximal computability structures", CCA 2018 presentation slides:
Copyright © 2018, Konrad Burnik