Author Archives: Konrad

CCA 2024 Conference

This week, during my vacation, I attended the Twenty-First International Conference on Computability and Complexity in Analysis. It was held at Swansea in Wales, UK. There I presented joint work with Zvonko Iljazović and Lucija Validžić. The title of the presentation was Computability of One-point Metric Bases. The slides can be found here.

Some photos from Swansea, including the Bay Campus can be found below.

Slides

CCA_2024_Burnik_Iljazovic_Validzic

CiE 2024 Conference

Leave a reply

On 8-12 July 2024, I attended online the Computability in Europe Conference 2024 held in Amsterdam. There were many interesting talks. Link to proceedings can be found here. Some of the recorded sessions can be found here.

Split-Complex Numbers as a Clifford Algebra

Leave a reply

The split-complex numbers are a special case of Clifford Algebra. This can be seen as follows. Let $X = \mathbb{R}^1$ . Let $e_1 = \langle a \rangle$ with $a \not = 0$ be a basis element of $\mathbb{R}^1$ . Then the Clifford Algebra $\mathcal{C}(\mathbb{R}^1)$ is defined as follows. The elements of the Clifford algebra are $\alpha + \beta e_1$ . Setting the rule for the Clifford product $e_1 \vee e_1$ as

(1) $\begin{equation*}e_1 \vee e_1 = 1\end{equation*}$

yields

$(\alpha_1 + \beta_1 e_1) \vee (\alpha_2 + \beta_2 e_1) = (\alpha_1 \alpha_2 + \beta_1 \beta_2) + (\alpha_1 \beta_2 + \beta_1 \alpha_2) e_1$

The isomorphism is $1 \mapsto 1$ , $e_1 \mapsto j$ . On the other hand, setting the rule to $e_1 \vee e_1 = 0$ or $e_1 \vee e_1 = -1$ in (1) yields a correspondence with dual-numbers or complex numbers respectively. I am planning to expand on this fact in one of the subsequent posts.

Implementation of Faster Complex Matrix Multiplication via Split-Complex Numbers

Leave a reply

In my previous post, I showed that split-complex numbers can be used to speed up complex matrix multiplication.

In this post I will do a quick measurement on exactly how much faster is the new approach when compared to the naive implementation in practice. Since we are using 3 real matrix multiplications in the new approach as opposed to 4 in the naive approach we would expect up to 25% improvement in the runtime. We can easily implement and test this by using Python's NumPy library. In the following listing the hyperbolic_matrix_mult function is the new approach that uses split-complex numbers and complex_matrix_mult is the function implementing the naive complex matrix multiplication.

# matrix_mult.py

import numpy as np

def hyperbolic_matrix_mult(Z1, Z2, W1, W2):
    X = 0.5 * (Z1 + Z2).dot(W1 + W2)
    Y = 0.5 * (Z1 - Z2).dot(W1 - W2)
    return X + Y - 2.0 * Z2.dot(W2), X - Y

def complex_matrix_mult(Z1, Z2, W1, W2):
    return Z1.dot(W1) - Z2.dot(W2), Z1.dot(W2) + Z2.dot(W1)

I will be running the test on my MacBook laptop with the following specs:

Hardware Overview:

  Model Name:                   MacBook Pro
  Model Identifier:             MacBookPro13,3
  Processor Name:               Quad-Core Intel Core i7
  Processor Speed:              2,6 GHz
  Number of Processors:         1
  Total Number of Cores:        4
  L2 Cache (per Core):          256 KB
  L3 Cache:                     6 MB
  Hyper-Threading Technology:   Enabled
  Memory:                       16 GB

The test will be as follows. First, we will generate four random real square matrices of order 10K. We use large matrices because we want the cost of multiplying the matrices to be the dominant factor in the runtime. Then, since the Jupyter notebook has nice features for timing the code, we can spin up a Jupyter notebook and perform the timing with the timeit command available as part of Jupyter. We will call timeit on both functions that will, by default, run the multiplication 7 times and calculate the mean and standard deviation of the collected run-times. This is all done in the following Jupyter Notebook snippet.

import numpy as np
from matrix_mult import hyperbolic_matrix_mult, complex_matrix_mult

n = 10000
A = np.random.rand(n, n)
B = np.random.rand(n, n)
C = np.random.rand(n, n)
D = np.random.rand(n, n)

%timeit hyperbolic_matrix_mult(A, B, C, D)
%timeit complex_matrix_mult(A, B, C, D)

After running this for about 45 minutes on my machine, here are the results. The first line shows the runtime of the method using split-complex numbers and the second one is the runtime of the naive complex matrix implementation.

49.9 s ± 388 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
1 min 2s ± 985 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

Already from this simple test we see that the improvement in time of the new algorithm over naive complex multiplication is about 20% which is not bad. Stay tuned for more thourough testing in the next post.

Faster Complex Matrix Multiplication via Split-Complex Numbers

Leave a reply

Here is a nice application of split-complex numbers. Let $Z_1 = A + i B$ and $Z_2 = C + i D$ be complex matrices. Their product is defined as

$Z_1 Z_2 = (A + i B) (C + iD) = (A C - B D) + i(AD + BC)$

which requires 4 real matrix multiplications. Here I will show that we can do this with 3 real matrix multiplications by using split-complex numbers.

First, by taking split-complex matrices $W_1 = A + j B$ and $W_2 = C + j D$ and rewriting them in basis $\{\iota, \iota^*\}$ as follows

$\begin{align*}W_1 & = (A+B) \iota + (A-B) \iota^* \\W_2 &= (C+D) \iota + (C-D) \iota^*\end{align*}$

we have

$W_1 W_2 = (A+B)(C+D) \iota + (A-B)(C-D) \iota^*$

which requires only 2 real matrix multiplications. This all follows from my previous post.

Let us now define

$\begin{align*}X & := \frac{1}{2} (A + B) (C + D) \\ Y & := \frac{1}{2} (A - B) (C - D).\end{align*}$

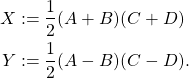
We have

$W_1 W_2 = (X + Y ) + j (X - Y).$

But now, since

$W_1 W_2 = (AC + BD) + j (AD + BC)$

then by comparison $AC + BD = X + Y$ and $AD + BC = X - Y$ .

Finally, from this and the fact $AC - BD = X + Y - 2 BD$ we have

$Z_1 Z_2 = (X + Y - 2 BD) + i(X - Y)$

which requires only 3 real matrix multiplications, namely $(A+B)(C+D)$ , $(A-B)(C-D)$ and $BD$ .

EDIT: A simple implementation of this approach can be found here.

This blog now runs on a new server

The blog has migrated to a new server yesterday! It was running on an old server with outdated software since 2013. Special thanks to my brother Kristijan for jumping in with his expertise to do a quick setup and migration of the blog to the new and improved server!

Enjoy the speed and stability of the new blog!

Article on Dense Computability Structures

On December 9 2020 the joint work with professor Zvonko Iljazović on dense computability structures was finally reviewed and accepted for publication in Journal of Complexity. The link to the article can be found here.

This work was done prior to my employment at Amazon.

Split-complex numbers revisited

A split-complex number is an algebraic expression of the form $x + j y$ where $x, y \in \mathbb{R}$ and $j^2 = + 1$ where $j \not = \pm 1$ . We can write a split-complex number simply as a pair of real numbers $(x,y)$ . Adding two split-complex numbers when represented as pairs is done component-wise. Hence, given $(a, b)$ and $(c, d)$ addition is defined as

$(a,b) + (c,d) = (a+c, b+d).$

However, the product of two split-complex numbers is not defined component-wise since

$(a,b) \cdot (c,d) = (ac + bd, ad + bc).$

One nice property of split-complex numbers is that we can change their representation in order to make multiplication component-wise as well.

Let

$\begin{align*}\iota = \frac{1 + j}{2} \ \mbox{ and } \ \iota^{*} = \frac{1 - j}{2}.\end{align*}$

Now each hyperbolic number $z = a + j b$ can uniquely be written in terms of
${\iota, \iota^* }$ as follows.

$z = (a + b) \iota + (a - b) \iota^{*}$

From here, the multiplication of two numbers $\tilde{z_1} = a \iota + b \iota^{*}$ and $\tilde{z_2} = c \iota + d\iota^{*}$ is now given component-wise by

$\tilde{z_1} \tilde{z_2} = a c \iota + b d \iota^{*}$

In this sense the transformed split-complex numbers algebraically behave just like two copies of real numbers since the algebraic operations are performed in each copy independently. More on this alternative representation of split-complex numbers in subsequent posts.

CCA 2019 Conference

Leave a reply

The CCA 2019 Conference was held in Zagreb, Croatia. I was one of the organizers as well as a presenter. I have presented joint work with Zvonko Iljazović.

Density_of_maximal_computability_structu

Investigations into infinite metric bases (Part 2/2)

In Part 1 I posed the following question:

"Does there exist a metric space $(X,d)$ such that it has an infinite metric base $A$ with the following properties:

$A$ is not dense;
for all finite metric bases $B$ of $(X,d)$ we have $B \not \subseteq A$ ?"

Let $d:\mathbb{R}^2 \times \mathbb{R}^2 \rightarrow \mathbb{R}$ be defined as

$d((x_1,x_2), (y_1, y_2)) = \max(|x_1 - y_1|, |x_2-y_2|)$

for all $(x_1, x_2), (y_1, y_2) \in \mathbb{R}^2$ . Then $d$ is a metric on $\mathbb{R}^2$ , denoted by $d_\infty$ and $(\mathbb{R}^2, d_\infty)$ is a metric space.

After a brief chat with professor Zvonko Iljazović, he proposed the metric space $(\mathbb{R}^2,d_\infty)$ and the integer lattice $\mathbb{Z}^2$ as the candidate for such a set. Here I will explain why this set is a good candidate.

Let $A = \mathbb{Z}^2$ . Then $A$ is a countable set, which is not dense in $\mathbb{R}^2$ which can be seen by taking for example $x = (1/2,1/2)$ and $\epsilon = 1/4$ then $B(x,\epsilon) \cap A = \emptyset$ . By [1] the space $(\mathbb{R}^2, d_\infty)$ does not have a finite metric base, therefore $A$ itself can not contain a finite metric base. What is left to prove is that $\mathbb{Z}^2$ is a metric base for $(\mathbb{R}^2, d_\infty)$ . The rest of this blog post is concerned with proving this fact.

First, note that the following result was mentioned briefly in our CCA 2018 presentation.

Proposition 1. Let $\{a,b,c\} \in [0,1]\times[0,1]$ such that either $a=(0,0)$ , $b = (1,1)$ or $a=(0,1)$ , $b = (1,0).$ Let $c \not \in \overline{ab}$ . Then $\{a,b,c\}$ is a metric base for $([0,1]\times[0,1], d_\infty)$ .

Interestingly enough, the article [1] already gives a complete characterisation of finite metric bases for squares in the digital plane for a couple of metrics including $d_\infty$ . My conjecture is that this also gives a complete characterisation of finite metric bases for $([0,1]\times[0,1], d_\infty)$ however, this is a topic for another blog post. For now, it seems that the result stated in Proposition 1 coincides with some parts of results from [1] and as such will be sufficient for our needs.

We will also need the following claim, which is straightforward to establish.

Proposition 2. Let $(X,d_X)$ and $(Y,d_Y)$ be metric spaces. If $\{a_0,\dots,a_n\}$ is a metric base for $(X, d)$ and $\phi : X \rightarrow Y$ is an onto mapping such that there exists $\lambda > 0$ with the property

$d_Y(\phi(x), \phi(y)) = \lambda \cdot d_X(x, y),$

for all $x, y \in X$ , then $\{\phi(a_0),\dots,\phi(a_n)\}$ is a metric base for $(Y, d_Y)$ .

By using Proposition 2 we can now easily find a metric base for an arbitrary square $[\alpha,\beta]\times[\alpha,\beta]$ where $\alpha< \beta$ by using the known result of Proposition 1 and finding a suitable map $\phi : [0,1]\times[0,1]\rightarrow [\alpha,\beta]\times[\alpha,\beta]$ .

Proposition 3. Let $\{a,b,c\}$ be a metric base for $([0,1]\times[0,1], d_\infty)$ . Let $\phi :[0,1]\times[0,1] \rightarrow [\alpha,\beta]\times[\alpha,\beta]$ where $\alpha < \beta$ be defined as

$\phi(x_1,x_2) = ((1-x_1)\alpha + x_1 \beta, (1-x_2)\alpha + x_2 \beta))$

for all $(x_1,x_2) \in [0,1]\times[0,1]$ . Then $\{\phi(a), \phi(b), \phi(c)\}$ is a metric base for $([\alpha,\beta]\times[\alpha,\beta], d_\infty)$ .

Note that by setting $\lambda = \beta - \alpha$ it is easy to verify that $\phi$ defined in Proposition 3 satisfies the property of $\phi$ from Proposition 2.

Finally, we now have everything we need to prove that $\mathbb{Z}^2$ is indeed a metric base for $(\mathbb{R}^2, d_\infty)$ .

Proposition 4. $\mathbb{Z}^2$ is a metric base for $(\mathbb{R}^2, d_\infty)$ .

Proof.

Let $A =\mathbb{Z}^2$ . Let $x, y \in \mathbb{R}^2$ and assume that

$d_\infty(x,a) = d_\infty(y,a)$

for all $a \in A$ .

Note that we can always choose $\alpha<\beta$ such that $\alpha,\beta\in \mathbb{Z}^2$ and $x, y \in [\alpha,\beta]\times[\alpha,\beta]$ . Namely, we can take for example $M \in \mathbb{N}$ such that $M > \max(|x_1|,|x_2|,|y_1|,|y_2|)+1$ and set $S =\widehat{B}_\infty(0, M)$ . Now set $\alpha = -M$ and $\beta = M$ .

From Proposition 1, it follows that any three corners of the square $[0,1]\times[0,1]$ are a metric base for $([0,1]\times[0,1], d_\infty)$ . By Proposition 3 there is a map $\phi :[0,1]\times[0,1] \rightarrow [\alpha,\beta]\times[\alpha,\beta]$ such that $\{\phi(a), \phi(b), \phi(c)\}$ is a metric base for $[\alpha,\beta]\times[\alpha,\beta]$ . Since $\{\phi(a), \phi(b), \phi(c)\} \subset A$ , then $d_\infty(x,p) = d_\infty(y,p)$ for all $p\in \{\phi(a), \phi(b), \phi(c)\}$ implies $x = y$ .

Therefore, $A$ is a metric base for $(\mathbb{R}^2, d_\infty)$ .

Q.E.D.

References

Robert A. Melter and Ioan Tomescu "Metric Bases in Digital Geometry", Computer Vision, Graphics, and Image Processing Volume 25, Issue 1, January 1984, Pages 113-121 DOI: https://doi.org/10.1016/0734-189X(84)90051-3
Konrad Burnik, Zvonko Iljazović, "Effective compactness and uniqueness of maximal computability structures", CCA 2018 presentation slides:

Effective_compactness_and_uniqueness_of