Introduction
Back in 2015 I published an article [1] about the QR decomposition of a centrosymmetric real matrix. In 2016 I started thinking about the meaning of this decomposition and centrosymmetric matrices in general. I discovered that centrosymmetric matrices have a natural interpretation as split-complex matrices and even more, that the centrosymmetric QR decomposition of a matrix actually corresponds to a QR decompositon of a split-complex matrix for which the original matrix is it representation. In a certain sense, the centrosymmetric QR decomposition introduced in [1] of a real square matrix of order ![]() is equivalent to a QR decomposition of a corresponding split-complex square matrix of order
is equivalent to a QR decomposition of a corresponding split-complex square matrix of order ![]() . All these notions will be made precise in the following sections. This blog post is based on my own preprint.
. All these notions will be made precise in the following sections. This blog post is based on my own preprint.
Matrix representations
If ![]() is a finite-dimensional vector space then we denote by
is a finite-dimensional vector space then we denote by ![]() the set of all linear transformations
the set of all linear transformations ![]() . Recall that if
. Recall that if ![]() is an
is an ![]() -dimensional vector space and
-dimensional vector space and ![]() an ordered basis for
an ordered basis for ![]() , then every linear transformation
, then every linear transformation ![]() has an
has an ![]() matrix representation with respect to
matrix representation with respect to ![]() denoted
denoted ![]() . Further, for any two linear transformations
. Further, for any two linear transformations ![]() we have
we have ![]() . The standard ordered basis for
. The standard ordered basis for ![]() i.e. the basis
i.e. the basis ![]() is defined as
is defined as ![]() if
if ![]() and
and ![]() otherwise.
otherwise.
An algebra ![]() is an ordered pair
is an ordered pair ![]() such that
such that ![]() is a vector space over a field
is a vector space over a field ![]() and
and ![]() is a bilinear mapping called multiplication.
is a bilinear mapping called multiplication.
Let ![]() be an algebra. A representation of
be an algebra. A representation of ![]() over a vector space
over a vector space ![]() is a map
is a map ![]() such that
such that
![]() for all
for all ![]() .
.
Let ![]() denote the set of
denote the set of ![]() real matrices. If
real matrices. If ![]() is an
is an ![]() -dimensional vector space and
-dimensional vector space and ![]() an ordered basis for
an ordered basis for ![]() then every linear transformation
then every linear transformation ![]() has a matrix representation
has a matrix representation ![]() . For each
. For each ![]() we have
we have ![]() . Since
. Since ![]() is
is ![]() -dimensional, we have and ordered basis
-dimensional, we have and ordered basis ![]() and
and ![]() . A matrix representation of
. A matrix representation of ![]() with respect to
with respect to ![]() } is a map
} is a map ![]() such that
such that ![]() for all
for all ![]() . Further, we have
. Further, we have ![]() for all
for all ![]() . These are all well known notions from representation theory, for further information, one can consult one of the standard textbooks, for example see [3].
. These are all well known notions from representation theory, for further information, one can consult one of the standard textbooks, for example see [3].
Algebra of split-complex numbers
(1) ![]()
an algebra. This is the well known algebra of split-complex numbers. The split-complex numbers are also sometimes known as hyperbolic numbers.
Similarly as for the complex numbers, each real number
With this correspondence, the pair
Since
For a hyperbolic number ![]() we define the real part as
we define the real part as ![]() and hyperbolic part as
and hyperbolic part as ![]() .
.
For the module we set ![]() and we have
and we have ![]() for all
for all ![]() .
.
For an extensive overview of the theory of hyperbolic numbers as well of their usefulness in Physics one can check the literature, for example [2]. For the rest of this blog post, we shall refer to these numbers as split-complex numbers.
Centrosymmetric representation of split-complex matrices
By ![]() we denote the set of all
we denote the set of all ![]() split-complex matrices i.e. matrices in which entries are split-complex numbers. Note that
split-complex matrices i.e. matrices in which entries are split-complex numbers. Note that ![]() if and only if there exist
if and only if there exist ![]() real matrices
real matrices ![]() ,
, ![]() such that
such that ![]() . If
. If ![]() is a matrix then its transpose is defined as
is a matrix then its transpose is defined as ![]() for all
for all ![]() and is denoted with
and is denoted with ![]() . In the following we denote by
. In the following we denote by ![]() the
the ![]() identity matrix and by
identity matrix and by ![]() the
the ![]() zero matrix. Let
zero matrix. Let ![]() be defined as
be defined as ![]() for each
for each ![]() . Note that
. Note that ![]() . A matrix
. A matrix ![]() is upper-triangular if
is upper-triangular if ![]() for all
for all ![]() .
.
A real matrix ![]() is centrosymmetric if
is centrosymmetric if ![]() . An overview of centrosymmetric matrices can be found in [4]. We denote by
. An overview of centrosymmetric matrices can be found in [4]. We denote by ![]() the set of all
the set of all ![]() centrosymmetric real matrices.
centrosymmetric real matrices.
For the algebra ![]() of split-complex numbers the well-known matrix representation
of split-complex numbers the well-known matrix representation ![]() with respect to
with respect to ![]() is given by
is given by
(2) ![]()
It is straightforward to check that for all
Further, on the vector space ![]() there is a natural multiplication operation
there is a natural multiplication operation ![]() given by
given by
(3) ![]()
for all
Note that in the following whenever we have two matrices ![]() , their product shall explicitly be written with a dot '
, their product shall explicitly be written with a dot '![]() ', e.g.
', e.g. ![]() to indicate multiplication defined in (3). Otherwise, if
to indicate multiplication defined in (3). Otherwise, if ![]() we simply write
we simply write ![]() .
.
To state and prove our main result, we shall need the following well known characterization of centrosymmetric matrices.
Proposition 1:
Let ![]() . Then
. Then ![]() if and only if there exist
if and only if there exist ![]() such that
such that
(4) ![]()
Proof:
Suppose
![]()
Since
*** QuickLaTeX cannot compile formula:
\[\begin{bmatrix}\ & J \\J & \\end{bmatrix}\begin{bmatrix}X & Y \\W & Z\end{bmatrix} =\begin{bmatrix}X & Y \\W & Z\end{bmatrix}\begin{bmatrix}\ & J \\J & \\end{bmatrix}\]
*** Error message:
\begin{bmatrix} on input line 17 ended by \end{equation*}.
leading text: ...begin{bmatrix}\ & J \\J & \\end{bmatrix}\]
Missing $ inserted.
leading text: ...begin{bmatrix}\ & J \\J & \\end{bmatrix}\]
Missing } inserted.
leading text: ...begin{bmatrix}\ & J \\J & \\end{bmatrix}\]
Missing \cr inserted.
leading text: ...begin{bmatrix}\ & J \\J & \\end{bmatrix}\]
Missing $ inserted.
leading text: ...begin{bmatrix}\ & J \\J & \\end{bmatrix}\]
Missing } inserted.
leading text: ...begin{bmatrix}\ & J \\J & \\end{bmatrix}\]
Missing \right. inserted.
leading text: ...begin{bmatrix}\ & J \\J & \\end{bmatrix}\]
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
This is equivalent to
![Rendered by QuickLaTeX.com \[\begin{bmatrix}JW & JZ \\JX & JY\\end{bmatrix} =\begin{bmatrix}YJ & XJ \\ZJ & WJ\end{bmatrix}\]](https://konrad.burnik.org/wordpress/wp-content/ql-cache/quicklatex.com-dd5627f494d4bca7581085523a98716c_l3.png)
We now have
![]()
Now, by choosing
Conversely, suppose ![]() has the form (4). It can easily be shown by block-matrix multiplication that
has the form (4). It can easily be shown by block-matrix multiplication that ![]() , hence
, hence ![]() is centrosymmetric.
is centrosymmetric.
QED.
(5) ![]()
is a matrix representation of
Proof:
Let ![]() and
and ![]() be such that
be such that ![]() and
and ![]() .
.
We now have
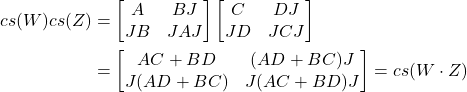
which proves the claim.
QED.
Proposition.
Let ![]() . Then
. Then ![]() .
.
Proof.
Let ![]() . Then
. Then
![]()
On the other hand, keeping in mind that
![]()
Hence,
QED.
Proposition.
The map ![]() is a bijection.
is a bijection.
Proof.
Injectivity. Let ![]() and
and ![]() and
and ![]() . From this,
. From this,
it follows that ![]() or
or ![]() . Assume that
. Assume that ![]() . Then
. Then
![]()
Since
We conclude that
Surjectivity. Let ![]() . By proposition 1 we can find matrices
. By proposition 1 we can find matrices ![]() and
and ![]() such that (4) holds. But then
such that (4) holds. But then ![]() and since
and since ![]() was arbitrary, we conclude that
was arbitrary, we conclude that ![]() is surjective.
is surjective.
Now, injectivity and surjectivity of ![]() imply by definition that
imply by definition that ![]() is a bijection.
is a bijection.
QED.
Correspondence of QR decompositions
Definition:
Let ![]() . A pair
. A pair ![]() with
with ![]() is a QR decomposition of
is a QR decomposition of ![]() over
over ![]() if the following holds:
if the following holds:
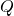 is orthogonal, i.e.
is orthogonal, i.e. 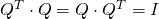 ,
,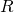 is upper-triangular,
is upper-triangular,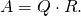
The notion of a ![]() double-cone matrix was introduced by the author in [1].
double-cone matrix was introduced by the author in [1].
Here we state the definition in block-form for the case of ![]() .
.
Definition:
Let ![]() . Then
. Then ![]() is a double-cone matrix iff there exist
is a double-cone matrix iff there exist ![]() both upper-triangular such that
both upper-triangular such that
![]()
Definition:
Let ![]() . A pair
. A pair ![]() , with
, with ![]() is a centrosymmetric QR decomposition of
is a centrosymmetric QR decomposition of ![]() if the following holds:
if the following holds:
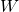 is orthogonal matrix,
is orthogonal matrix,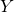 is double-cone matrix,
is double-cone matrix,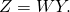
The algorithm to obtain an approximation of a centrosymmetric QR decomposition of a given centrosymmetric matrix ![]() was given in [1].
was given in [1].
The following theorem provides one interpretation of the centrosymmetric QR decomposition, in the case of square centrosymmetric matrices of even order by establishing the equivalence of their centrosymmetric QR decomposition with the QR decomposition of the corresponding split-complex matrix.
Theorem 1 (QR decomposition correspondence):
Let ![]() . Then
. Then ![]() is a QR decomposition of
is a QR decomposition of ![]() if and only if
if and only if
![]()
Proof.
Let ![]() be a QR decomposition of
be a QR decomposition of ![]() .
.
Let ![]() and
and ![]() . We have
. We have
![]()
Since
From this we have
Finally, we have
a centrosymmetric QR decomposition of
Conversely, let ![]() . If
. If ![]() is a centrosymmetric QR decomposition of
is a centrosymmetric QR decomposition of ![]() then
then ![]() where
where ![]() is centrosymmetric and orthogonal and
is centrosymmetric and orthogonal and ![]() is a double-cone matrix.
is a double-cone matrix.
From the fact that ![]() is centrosymmetric we have (by Proposition 1) that
is centrosymmetric we have (by Proposition 1) that
![]()
Now the property of
(6) ![]()
On the other hand, we have
(7) ![]()
First we prove that
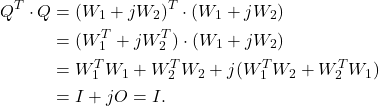
The matrix
![]()
where both
Finally, let us prove that ![]() . We have
. We have
![]()
We conclude that
QED.
Example:
Let
![]()
Note that
(8) ![]()
We have
![Rendered by QuickLaTeX.com \[{cs}(A) = {cs}(W + jZ) = \begin{bmatrix}W & ZJ \\JZ & JWJ\end{bmatrix}= \begin{bmatrix}1 & 2 & 3 & 2 \\3 & 4 & 5 & 4 \\4 & 5 & 4 & 3 \\2 & 3 & 2 & 1\end{bmatrix}\]](https://konrad.burnik.org/wordpress/wp-content/ql-cache/quicklatex.com-1c69ab9d656b5f8fe677e72f6445a893_l3.png)
By applying the
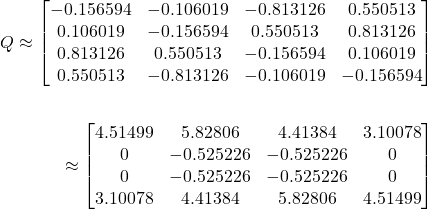
Applying ![]() to
to ![]() and
and ![]() yields:
yields:
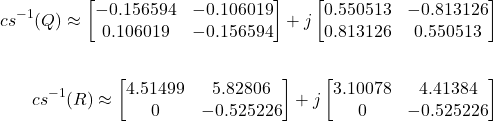
with
Conclusion
We introduced the standard centrosymmetric representation ![]() for split-complex matrices. Using this representation we proved that a QR decomposition of a square split-complex matrix
for split-complex matrices. Using this representation we proved that a QR decomposition of a square split-complex matrix ![]() can be obtained by calculating the centrosymmetric QR decomposition introduced by the author in [1] of its centrosymmetric matrix representation
can be obtained by calculating the centrosymmetric QR decomposition introduced by the author in [1] of its centrosymmetric matrix representation ![]() .
.
References
- Burnik, Konrad. A structure-preserving QR factorization for centrosymmetric real matrices,
Linear Algebra and its Applications 484(2015) 356 - 378 - Catoni, Francesco and Boccaletti, Dino and Cannata, Roberto and Catoni, Vincenzo and Zampeti, Paolo, Hyperbolic Numbers. Geometry of Minkowski Space-Time Springer Berlin Heidelberg Berlin, Heidelberg, (2011) 3–23 ISBN: 978-3-642-17977-8
- Curtis, Charles W.; Reiner, Irving. Representation Theory of Finite Groups and Associative Algebras, John Wiley & Sons (Reedition2006 by AMS Bookstore), (1962) ISBN 978-0-470-18975
- James R. Weaver. Centrosymmetric (Cross-Symmetric) Matrices,Their Basic Properties, Eigenvalues, and Eigenvectors, The American Mathematical Monthly, Mathematical Association of America, (1985) 10-92, 711–717 ISSN: 00029890, 19300972 doi:10.2307/2323222
Copyright © 2018, Konrad Burnik