Here is a nice application of split-complex numbers. Let ![]() and
and ![]() be complex matrices. Their product is defined as
be complex matrices. Their product is defined as
![]()
which requires 4 real matrix multiplications. Here I will show that we can do this with 3 real matrix multiplications by using split-complex numbers.
First, by taking split-complex matrices ![]() and
and ![]() and rewriting them in basis
and rewriting them in basis ![]() as follows
as follows
![]()
we have
![]()
which requires only 2 real matrix multiplications. This all follows from my previous post.
Let us now define
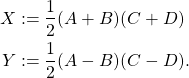
We have
![]()
But now, since
![]()
Finally, from this and the fact ![]() we have
we have
![]()
EDIT: A simple implementation of this approach can be found here.