Let ![]() be a metric space. Let
be a metric space. Let ![]() be such that for all
be such that for all ![]() the following implication holds:
the following implication holds:
![]()
then we say ![]() is a metric base for
is a metric base for ![]() . A sequence
. A sequence ![]() in
in ![]() is called a dense sequence iff
is called a dense sequence iff ![]() is a dense set. A metric base
is a dense set. A metric base ![]() is a finite metric base iff
is a finite metric base iff ![]() is a finite set. Finding a finite metric base (if it exists) in a general metric space is already an interesting challenge and this will be explored in more detail in another post. Some information about how finite metric bases relate to computability can be found in another post. The question of existence of infinite metric bases however seems a bit less challenging due to the following easy result.
is a finite set. Finding a finite metric base (if it exists) in a general metric space is already an interesting challenge and this will be explored in more detail in another post. Some information about how finite metric bases relate to computability can be found in another post. The question of existence of infinite metric bases however seems a bit less challenging due to the following easy result.
Proposition: Let ![]() be a metric space. Let
be a metric space. Let ![]() be a dense sequence in
be a dense sequence in ![]() . Then
. Then ![]() is a metric base for
is a metric base for ![]() .
.
Proof. Let ![]() be a dense sequence and set
be a dense sequence and set ![]() . Let
. Let ![]() . Suppose
. Suppose ![]() for all
for all ![]() . Since
. Since ![]() is dense, there exists a sequence
is dense, there exists a sequence ![]() in
in ![]() such that
such that ![]() . This is equivalent to
. This is equivalent to ![]() . Since
. Since ![]() for all
for all ![]() we have
we have ![]() .
.
Set ![]() ,
, ![]() and
and ![]() for all
for all ![]() . From the triangle inequality and non-negativity of the metric we now have
. From the triangle inequality and non-negativity of the metric we now have ![]() for all
for all ![]() .
.
Since ![]() and
and ![]() , we have by the squeeze theorem
, we have by the squeeze theorem ![]() , therefore
, therefore ![]() which implies
which implies ![]() . We conclude that
. We conclude that ![]() is a metric base for
is a metric base for ![]() .
.
Q.E.D.
Obviously, by set inclusion we have that every ![]() that contains a metric base is a metric base. What about metric bases which are not dense in
that contains a metric base is a metric base. What about metric bases which are not dense in ![]() and also do not contain a finite metric base? Formally, we have the following question:
and also do not contain a finite metric base? Formally, we have the following question:
Question: Does there exist a metric space ![]() such that it has an infinite metric base
such that it has an infinite metric base ![]() with the following properties:
with the following properties:
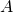 is not dense;
is not dense;- for all finite metric bases
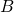 of
of 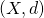 we have
we have 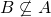 ?
?
More about that in the following posts.