What is Computable analysis anyway?
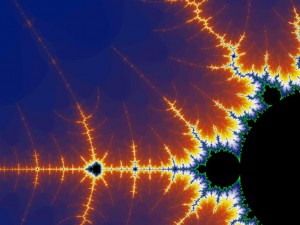
Roger Penrose in his book "The emperors new Mind" asked an interesting question regarding the Mandelbrot set: "Is the Mandelbrot set recursive?" The term "recursive" is an old name for "computable" and has nothing to do with recursion in programming.
Classical computability theory (also known as recursion theory) is a branch of mathematical logic that deals with studying what functions ![]() are computable. Computable analysis is in some sense an extension of this theory. It is a branch of mathematics that applies computability theory to problems in mathematical analysis. It is concerned with questions of effectivity in analysis and its main goal is to find what parts of analysis can be described by an algorithmic procedure, one of the basic questions being what functions
are computable. Computable analysis is in some sense an extension of this theory. It is a branch of mathematics that applies computability theory to problems in mathematical analysis. It is concerned with questions of effectivity in analysis and its main goal is to find what parts of analysis can be described by an algorithmic procedure, one of the basic questions being what functions ![]() are computable? (note the domain and codomain are now the reals).
are computable? (note the domain and codomain are now the reals).
Computable reals
Suppose we take a real number ![]() . Is
. Is ![]() computable? What do we mean by
computable? What do we mean by ![]() being computable? If we can find an algorithm
being computable? If we can find an algorithm ![]() that calculates for each input
that calculates for each input ![]() a rational approximation
a rational approximation ![]() of
of ![]() ; and such that the sequence
; and such that the sequence ![]() "converges fast" to
"converges fast" to ![]() then we say that
then we say that ![]() is a computable real. More precisely, a real number
is a computable real. More precisely, a real number ![]() is computable iff there exists a computable function
is computable iff there exists a computable function ![]() such that
such that ![]() for each
for each ![]() . For example, every rational number is computable. The famous number
. For example, every rational number is computable. The famous number ![]() is computable, and in our previous post we proved that
is computable, and in our previous post we proved that ![]() is computable. It turns out that the set of computable reals, denoted by
is computable. It turns out that the set of computable reals, denoted by ![]() is a field with respect to addition and multiplication. But there exist real numbers which are not computable. This is easy to see as there is only a countable number of computable functions
is a field with respect to addition and multiplication. But there exist real numbers which are not computable. This is easy to see as there is only a countable number of computable functions ![]() , and since we know that
, and since we know that ![]() is uncountable, so we have more real numbers than we have possible algorithms, we conclude that there must be a real number that is not computable. One example of an uncomputable real is the limit of a Specker sequence. And one other interesting one is the Chaitin constant. In fact, if we take any recursively enumerable but non-recursive set
is uncountable, so we have more real numbers than we have possible algorithms, we conclude that there must be a real number that is not computable. One example of an uncomputable real is the limit of a Specker sequence. And one other interesting one is the Chaitin constant. In fact, if we take any recursively enumerable but non-recursive set ![]() , then the number
, then the number ![]() is an example of a real number which is not computable.
is an example of a real number which is not computable.
Computable sequences of reals
If we have a sequence of computable reals ![]() (and hence a sequence of algorithms) we may ask if this sequence is computable i.e. is there a single algorithm that describes the whole sequence? If there exists a computable function
(and hence a sequence of algorithms) we may ask if this sequence is computable i.e. is there a single algorithm that describes the whole sequence? If there exists a computable function ![]() such that
such that
![]()
for each ![]() then we say that
then we say that ![]() is a computable sequence of reals. We have seen that each rational number is computable, but this is not true for sequences of rational numbers! One example of a sequence that has each term computable and also computable as a sequence of reals, but it is not computable as a sequence of rationals is the following [Pour-el, Richards]:
is a computable sequence of reals. We have seen that each rational number is computable, but this is not true for sequences of rational numbers! One example of a sequence that has each term computable and also computable as a sequence of reals, but it is not computable as a sequence of rationals is the following [Pour-el, Richards]:
Example:
Take any recursively enumerable but non-recursive set ![]() and let
and let ![]() be a one-to-one recursive function which enumerates
be a one-to-one recursive function which enumerates ![]() .
.
Let ![]() be given by
be given by
![]()
Then ![]() is not computable (as a sequence) of reals but
is not computable (as a sequence) of reals but ![]() is not computable as a sequence of rationals.
is not computable as a sequence of rationals.
Computable real functions
Real functions which are the main object of study in analysis can be studied in this computability setting, a function ![]() is computable iff
is computable iff
- it maps computable sequences to computable sequences i.e.
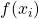 is computable for every computable sequence
is computable for every computable sequence 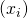 ;
; - it is effectively uniformly continuous;
The fundamental theorem of computable analysis is that every computable real function is continuous.
There is also a notion of computability for the process of integration, derivation, solving partial differential equations, etc. and we shall look into that topic in another post.
Computable subsets of the Euclidean space
Next, let's look at the subsets of the euclidean space ![]() and ask a simple question: what subsets are computable? First, note that saying
and ask a simple question: what subsets are computable? First, note that saying ![]() is computable iff its indicator function
is computable iff its indicator function
![Rendered by QuickLaTeX.com \[\chi_S(x) =\begin{cases} 1, & x \in S \\ 0, & x \not \in S \end{cases}\]](https://konrad.burnik.org/wordpress/wp-content/ql-cache/quicklatex.com-064bd0cca97592aa71745aad2444c6ab_l3.png)
is computable is not a useful definition since the indicator function is not continous except when ![]() or
or ![]() . A subset
. A subset ![]() of
of ![]() is computable iff the function
is computable iff the function ![]() defined as
defined as ![]() is a computable function. For example, take the unit circle in
is a computable function. For example, take the unit circle in ![]() .
.
![]()
. The distance function is
![]()
These are just some basic definitions and facts, but also interesting questions are studied in computable analysis like for example what mappings preserve computability of objects? Is for example the Mandelbrot set computable? What about Julia Sets? For them, there are nice results presented in the book "Computability of Julia Sets" by Braverman and Yampolsky. Although Julia Sets have been thoroughly researched in the book, for the Mandelbrot set we still don't know the answer.
Basically for anything we do in analysis (finding derivatives, integration, finding roots, solving PDEs ...) we may ask: "Is it computable?" and that is a topic for another post.
(to be continued)
Copyright © 2014, Konrad Burnik