#####################################################################
#
# Implementing the notion of Computable Set in the euclidean plane 
#
# Every weakly computable set in the euclidean plane is a set 
# of zeroes of some a computable function.
#
# Konrad Burnik, June 2017.
#
#####################################################################

from math import *
from decimal import *
import matplotlib.pyplot as plt

class ComputableSet:
    '''A computable subset of the euclidean plane is given by its computable function representing it.'''
    def f(self, x, y):
        '''A function whose zeroes represent this computable set. 
           For example: def f(x, y): return x**2 + y**2 - 1 has zeroes which represents a unit circle.
        '''
        raise Exception("Not implemented!")
    
    def points(self, k):
        return [(x/2**k, y/2**k) 
                        for y in range(-2**k, 2**k + 1) 
                        for x in range(-2**k, 2**k + 1) 
                        if Decimal(-1) / Decimal(2**k) < self.f(Decimal(x)/Decimal(2**k), Decimal(y)/Decimal(2**k)) < Decimal(1) / Decimal(2**k)]  class Circle(ComputableSet):
    def f(self, x, y):
        return x**2 + y**2 - Decimal(1/2)
class EllipticCurve(ComputableSet):
    def f(self, x, y):
        return x**2 + y**3 - Decimal(1/2)

def plot_set(s, k):
    points = s.points(k)
    x = list(map(lambda x : x[0], points))
    y = list(map(lambda x : x[1], points))

    plt.plot(x, y, 'ro')
    plt.show()

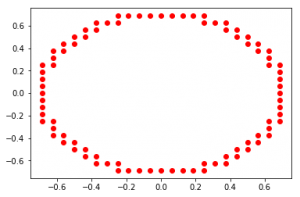
class Circle(ComputableSet):
    def f(self, x, y):
        return x**2 + y**2 - Decimal(1/2)

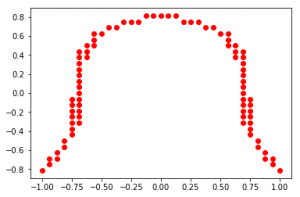
class EllipticCurve(ComputableSet):
    def f(self, x, y):
        return x**2 + y**3 - Decimal(1/2)

class ComputableSetUnion(ComputableSet):
    def __init__(self):
        self.A = ComputableSet()
        self.B = ComputableSet()
        
    def f(self, x, y):
        return self.A.f(x, y) * self.B.f(x, y)

+1

0